搜索到
29
篇与
的结果
-
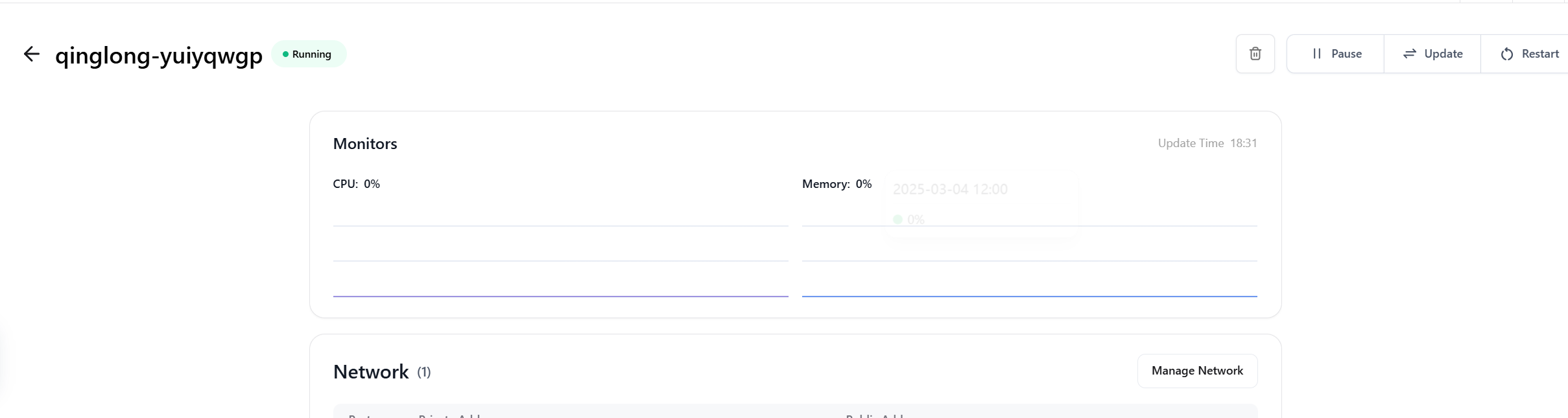
 阿里云大厂免费服务器-花语:手慢无 本文截稿的时候,因为人比较多,服务器有时候属于宕机的状态,但是我还是建议注册一下。宁可不能用,也不要错过的精神~Claw Cloud Run 是阿里云青春版 Claw Cloud 旗下,类似于 Vercel、Netlify 的在线开发平台,可以快速部署 Alist、Dify、frp 等程序,目前只需要绑定一个注册超过 180 天的 GitHub 账号,即可永久免费赠送 5 刀/月额度,可在每个可用区使用最多 4 vCPU、8GiB 内存、10GiB 硬盘资源,共提供 10GB 流量。你需要的就是准备一个超过180天的Github账号 一台电脑或者手机或者平板,即可享受免费的服务器这5刀额度并不能用来兑换 Hobby 套餐,而是在使用 Free 套餐时用来抵扣费用。比如在 Claw Cloud Run 的应用商店中一键安装 Alist 时,抵扣一天4分钱:Claw Cloud Run 为注册 GitHub 超过 180 天的用户,每月赠送 5 刀额度,可一键安装76款开源程序 3从应用商店来看,目前支持非常多常见的开源项目:AffiNEAlistanki-sync-serverchatbot-uiDbGateDeeplXDifyExcalidrawFlarumfrpGiteaHeyFormLobe ChatmemosMinecraftMinION8NOpen WebUI青龙面板RSSHubRustDeskStirling-PDFWordPress如果你有一些个人用途的项目需要跑一跑,还是非常划算的,毕竟免费。比如博主就是部署了一个青龙和wordpress虽然一直无法访问把 但是你就说是不是部署了 😁 本文就这了,水一篇把~~~~
阿里云大厂免费服务器-花语:手慢无 本文截稿的时候,因为人比较多,服务器有时候属于宕机的状态,但是我还是建议注册一下。宁可不能用,也不要错过的精神~Claw Cloud Run 是阿里云青春版 Claw Cloud 旗下,类似于 Vercel、Netlify 的在线开发平台,可以快速部署 Alist、Dify、frp 等程序,目前只需要绑定一个注册超过 180 天的 GitHub 账号,即可永久免费赠送 5 刀/月额度,可在每个可用区使用最多 4 vCPU、8GiB 内存、10GiB 硬盘资源,共提供 10GB 流量。你需要的就是准备一个超过180天的Github账号 一台电脑或者手机或者平板,即可享受免费的服务器这5刀额度并不能用来兑换 Hobby 套餐,而是在使用 Free 套餐时用来抵扣费用。比如在 Claw Cloud Run 的应用商店中一键安装 Alist 时,抵扣一天4分钱:Claw Cloud Run 为注册 GitHub 超过 180 天的用户,每月赠送 5 刀额度,可一键安装76款开源程序 3从应用商店来看,目前支持非常多常见的开源项目:AffiNEAlistanki-sync-serverchatbot-uiDbGateDeeplXDifyExcalidrawFlarumfrpGiteaHeyFormLobe ChatmemosMinecraftMinION8NOpen WebUI青龙面板RSSHubRustDeskStirling-PDFWordPress如果你有一些个人用途的项目需要跑一跑,还是非常划算的,毕竟免费。比如博主就是部署了一个青龙和wordpress虽然一直无法访问把 但是你就说是不是部署了 😁 本文就这了,水一篇把~~~~ -
 mdclub论坛搭建教程 今天出来的教程是mdclub的全系列的搭建教程,后期我会出APP的搭建教程。保姆的教程我就不出了,直接说大概 然后说需要注意的一些点把,下午我搭建了俩小时才出来的。也和第一次搭建mdclub有关系。这里我还想说一下为什么我最后选择了mdclub而不是discuz和其他这俩论坛。我在这里做一个对比mdclubdiscuz其他支出API不支持API个别支持大型无压力大型无压力很多停止维护界面简单模板多模板很少其实搭建和wordpress什么的基本都差不多。如果wordpress什么不会的话 那么建议看B站视频去学习了。接下来说一些注意点。1.就是php的选择是7.4+需要有fileinfo的拓展(必须有的)。如果没有的话,你根本无法下一步。2.伪静态的话 直接选择thinkphp即可,运行目录是public。如果不配置伪静态的话,就会发现install的时候是404页面。3.网站记得申请SSL,如果不申请的话,那么对于后面的app搭建api获取有一些麻烦,而且容易被抓取内容。基本的风格是比较简约干净的,符合我的审美,其实网页基本还是喂给了蜘蛛了。现在大多数我认为还是移动端的天下。与其纠结网站页面如何的话 比如好好配置APP。还有就是邮箱的配置。我找到了一个免费的STMP的邮箱网站,一天200封邮件,基本对于小型站点足够了。 😗 如果日注册真的上200的话。还缺什么STMP的小钱钱{card-describe title="网站详细地址我隐藏啦"}评论即可获取{/card-describe}隐藏内容,请前往内页查看详情
mdclub论坛搭建教程 今天出来的教程是mdclub的全系列的搭建教程,后期我会出APP的搭建教程。保姆的教程我就不出了,直接说大概 然后说需要注意的一些点把,下午我搭建了俩小时才出来的。也和第一次搭建mdclub有关系。这里我还想说一下为什么我最后选择了mdclub而不是discuz和其他这俩论坛。我在这里做一个对比mdclubdiscuz其他支出API不支持API个别支持大型无压力大型无压力很多停止维护界面简单模板多模板很少其实搭建和wordpress什么的基本都差不多。如果wordpress什么不会的话 那么建议看B站视频去学习了。接下来说一些注意点。1.就是php的选择是7.4+需要有fileinfo的拓展(必须有的)。如果没有的话,你根本无法下一步。2.伪静态的话 直接选择thinkphp即可,运行目录是public。如果不配置伪静态的话,就会发现install的时候是404页面。3.网站记得申请SSL,如果不申请的话,那么对于后面的app搭建api获取有一些麻烦,而且容易被抓取内容。基本的风格是比较简约干净的,符合我的审美,其实网页基本还是喂给了蜘蛛了。现在大多数我认为还是移动端的天下。与其纠结网站页面如何的话 比如好好配置APP。还有就是邮箱的配置。我找到了一个免费的STMP的邮箱网站,一天200封邮件,基本对于小型站点足够了。 😗 如果日注册真的上200的话。还缺什么STMP的小钱钱{card-describe title="网站详细地址我隐藏啦"}评论即可获取{/card-describe}隐藏内容,请前往内页查看详情 -
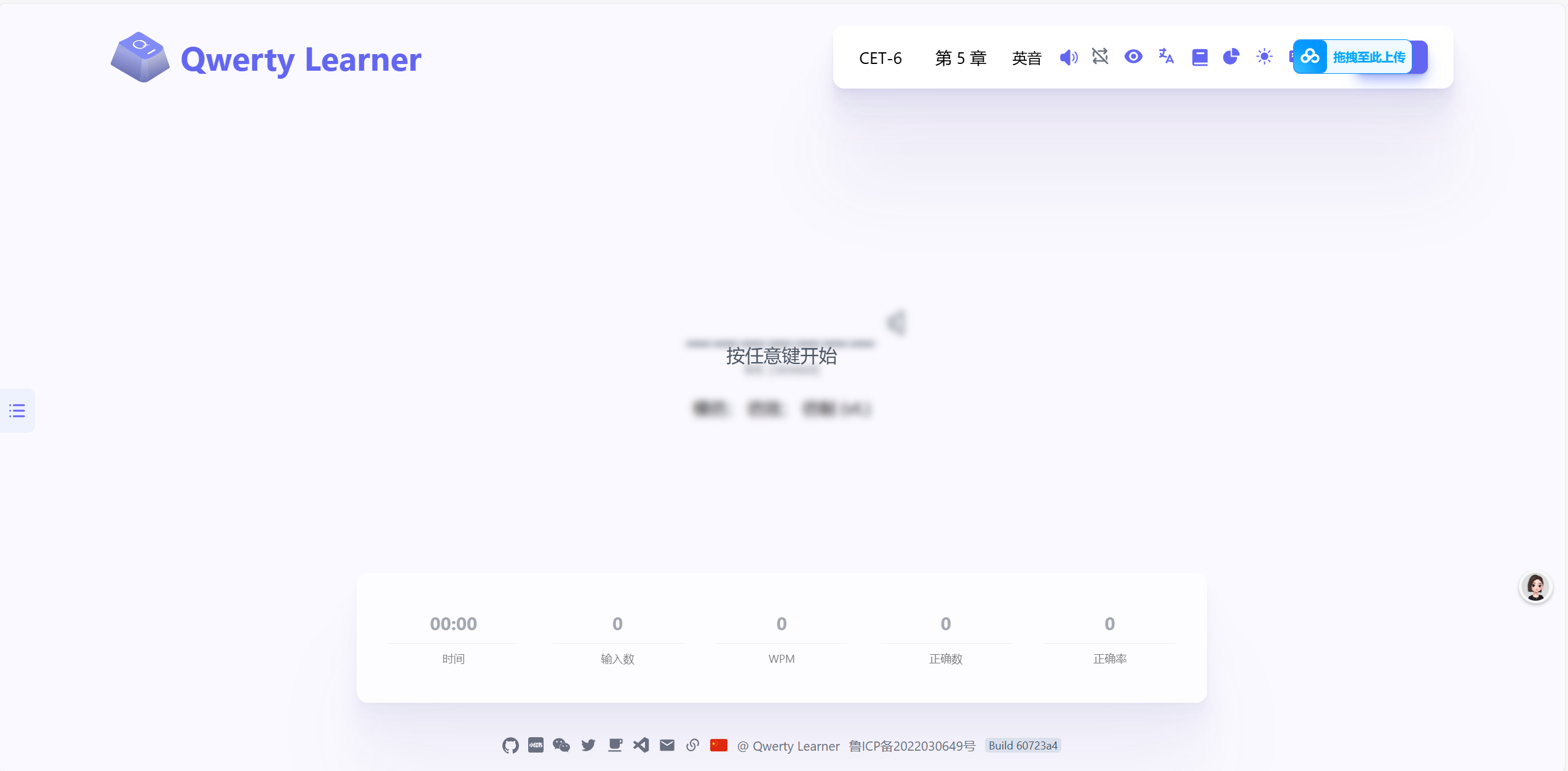
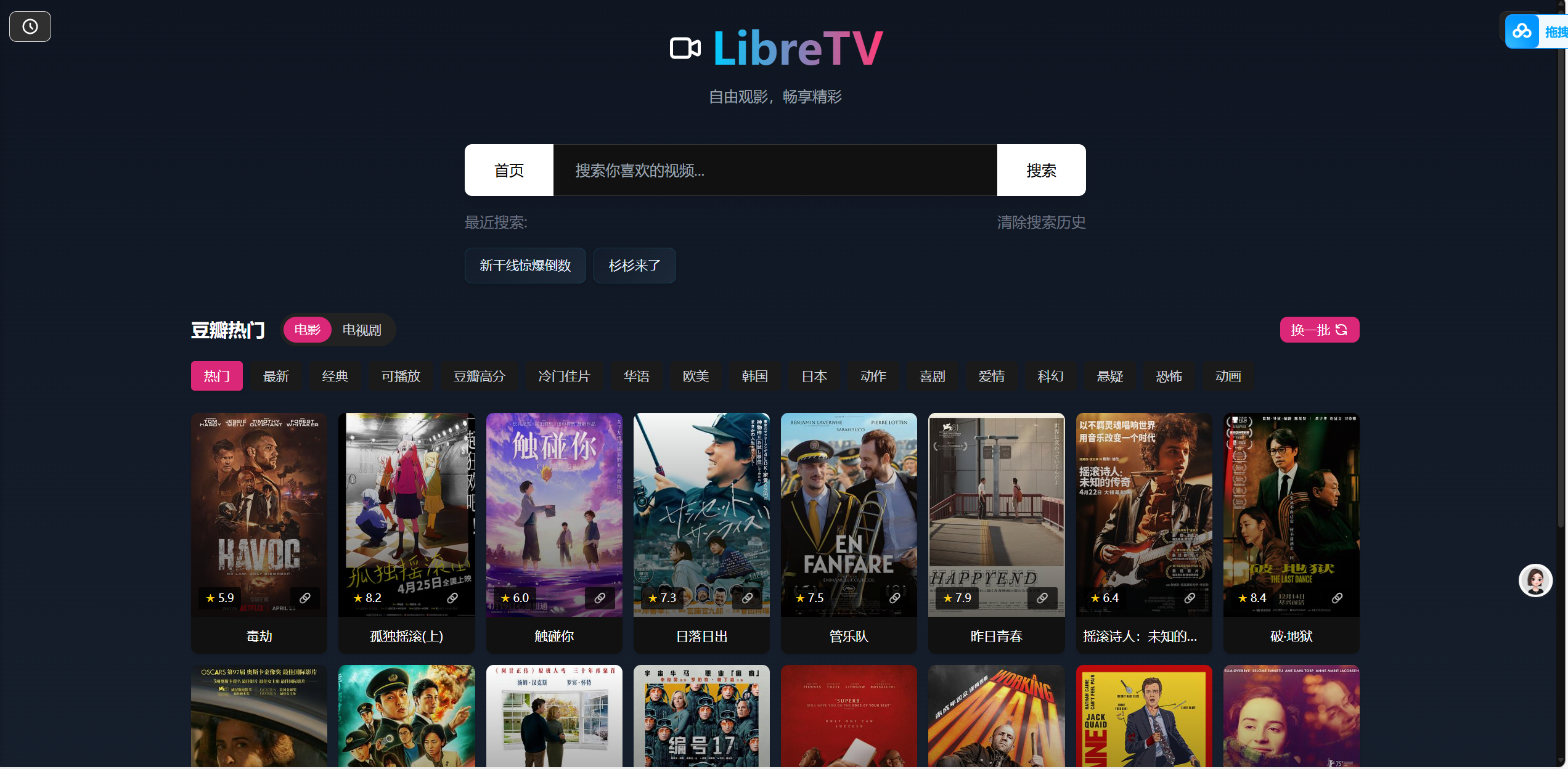
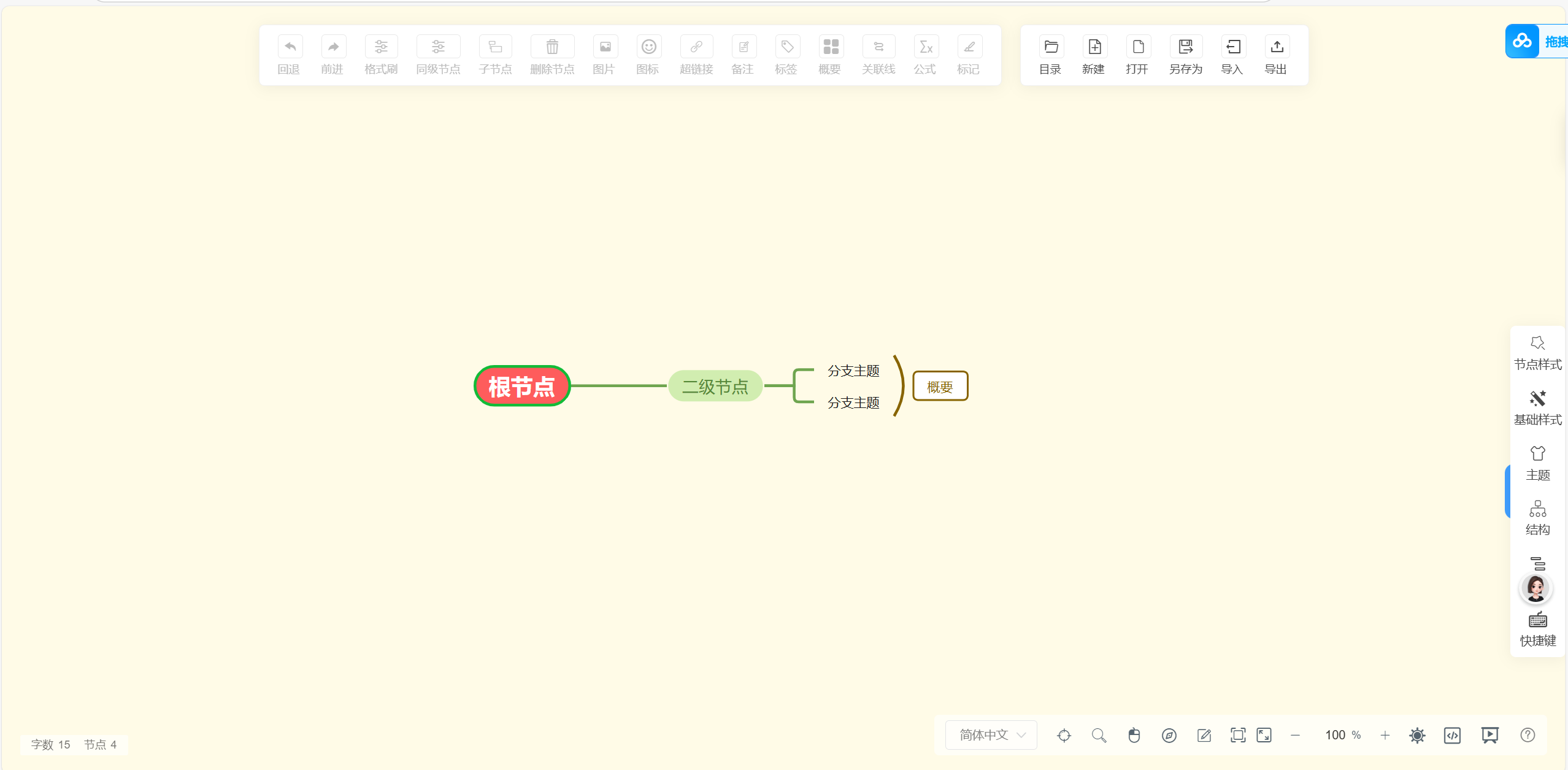
我发现了一些超级好用的网站 我最近发现了一些超级无敌好用的网站我在这里进行简单的汇总一些。首先就是我们的背单词网站,当然这个用的我们的开源项目-qwety learner 这个是专门为了经常使用电脑的同学来开发的网站,作者开源了项目,在Github上面下载即可去部署项目,当然我也是第一时间搭建好了,不过我搭建的利用的vercel。各位可以放心大胆的利用我的网站背诵单词,理论永久存在~ 背单词 接下来就是影视搜索网站,这个网站不是我搭建的 这个网站所有的资源源自网络,本网站不作任何的存储整理,如果访问的话 麻烦24H内删除所有的资源,本站不携带任何的数据,和站长没有任何的关系。我看了一下页面接口,调用的是豆瓣的热搜,总体说起来还不错把免费guan'y 接下来就是免费的思维导图网站了,同样也是免费的。导出来的格式有很多很多 我在这里不说话,我直接截图可以自行体验一下(第一次打开可能比较慢,但后面打开就会快了) 免费思维导图 接下来就是免费AI工具了。同样也是免费的但是这个又是不一样一点点,因为它基于的是openai的接口,因此需要去输入一些密钥,当然没有密钥的也可以评论区获取专属密钥~~~ AI网站



-
 苹果cms搭建教程2025年最新版本 教程列表1、下载苹果CMS2、安装苹果CMS3、安装苹果cms模板4、苹果CMS采集准备工作1、苹果cms源码2、购买服务器,安装宝塔面板3、购买域名搭建教程苹果cms安装教程1:下载苹果cms到本地2:安装好宝塔面板后,首先得安装PHP环境,一般版本的CMS都支持PHP7.2以上。例外还要安装 PHP 7.2 的扩展 SG11;我这里用PHP7.4。3:创建站点4:上传苹果CMS源码 解压5:访问域名,点击同意协议并安装系统6:配置数据库,点击立即安装完成后 进入后台发现进不去 这时候我们需要修改一下后台地址苹果CMS搭建安装教程,从下载到安装完整版7:修改后台地址,找到admin.php文件 修改文件名,修改完后我们进入后台: 域名/修改的名称.php。输入账号密码和验证码登录进行就可以进入后台界面。8:伪静态配置苹果CMS搭建安装教程,从下载到安装完整版苹果cms模板安装教程1:将下载好的模板压缩包上传到我们网站根目录下的-【tempalte】下并进行解压;2:登录后台,进入“系统”-“网站参数配置”,网站模板的地方选择刚刚上传的模板文件名称,点击保存就可以了。苹果CMS搭建安装教程,从下载到安装完整版苹果CMS采集教程1、依次点击【采集】-【自定义接口】-【添加】2、然后依次输入您在本站复制的资源站名称和地址3、点击【保存】按钮即可苹果CMS搭建安装教程,从下载到安装完整版如果资源站有提供专用的播放器,我们还需要添加一个播放器才行。如果资源站没提示就代表可以不用操作此步骤。1、我们需要去资源站直接下载或到采集接口栏目下载2、点击“视频”-“播放器”3、点击“导入”导入刚刚下载的播放器文件就可以了。绑定分类开始采集1、点击刚刚添加的采集接口,进入分类绑定页面2、绑定完成后就可以开始采集了3、可以自由选择采集当天、本周或者一次性采集全部。这里附上一些苹果cms的资源站,可能跑路,但是只能亲测到网站发布时间还在的
苹果cms搭建教程2025年最新版本 教程列表1、下载苹果CMS2、安装苹果CMS3、安装苹果cms模板4、苹果CMS采集准备工作1、苹果cms源码2、购买服务器,安装宝塔面板3、购买域名搭建教程苹果cms安装教程1:下载苹果cms到本地2:安装好宝塔面板后,首先得安装PHP环境,一般版本的CMS都支持PHP7.2以上。例外还要安装 PHP 7.2 的扩展 SG11;我这里用PHP7.4。3:创建站点4:上传苹果CMS源码 解压5:访问域名,点击同意协议并安装系统6:配置数据库,点击立即安装完成后 进入后台发现进不去 这时候我们需要修改一下后台地址苹果CMS搭建安装教程,从下载到安装完整版7:修改后台地址,找到admin.php文件 修改文件名,修改完后我们进入后台: 域名/修改的名称.php。输入账号密码和验证码登录进行就可以进入后台界面。8:伪静态配置苹果CMS搭建安装教程,从下载到安装完整版苹果cms模板安装教程1:将下载好的模板压缩包上传到我们网站根目录下的-【tempalte】下并进行解压;2:登录后台,进入“系统”-“网站参数配置”,网站模板的地方选择刚刚上传的模板文件名称,点击保存就可以了。苹果CMS搭建安装教程,从下载到安装完整版苹果CMS采集教程1、依次点击【采集】-【自定义接口】-【添加】2、然后依次输入您在本站复制的资源站名称和地址3、点击【保存】按钮即可苹果CMS搭建安装教程,从下载到安装完整版如果资源站有提供专用的播放器,我们还需要添加一个播放器才行。如果资源站没提示就代表可以不用操作此步骤。1、我们需要去资源站直接下载或到采集接口栏目下载2、点击“视频”-“播放器”3、点击“导入”导入刚刚下载的播放器文件就可以了。绑定分类开始采集1、点击刚刚添加的采集接口,进入分类绑定页面2、绑定完成后就可以开始采集了3、可以自由选择采集当天、本周或者一次性采集全部。这里附上一些苹果cms的资源站,可能跑路,但是只能亲测到网站发布时间还在的 -
 搭建苹果cms的一些感受 以下文字仅仅提供解决方案,所有图文字均源自网络,支持正版,人人有责。这也算是搭建苹果CMS很多次了,也有一些经验什么的了。这些简单说一些搭建苹果cms的终极方案,以及什么样的人适合搭建影视,什么样的人不适合影视首先就是如果你仅仅是为了自己看电影或者旁边人去看看电影,那么搭建苹果cms不是最佳的选择。现在市场上有很多开源的盒子,很多源。直接导入就可以用,如果不放心,可以投资的话 那么建议上NAS,或者其他的平替方案,总之苹果CMS,浪费时间。而且你搭建出来的不一定比别人好,别人切片,付费解析,各种方案一上,加载快。你反而得不偿失。接下来就是还有一种人不适合搞影视,就是如果搭建出是为了盈利,那么建议换一条赛道。这个盈利基本靠广告,但是能接到的广告,懂得都懂。如果你计划盈利的话 那么其实不太适合,建议换一条赛道。接下来什么样的人适合这个。首先就是如果你计划去公开网站进行SEO优化后引流之类的,那么影视适合,通过批量采集,吸引流量。其次就是如果是纯兴趣爱好,那么也适合,这里面门道有很多,很适合打法时间,或者说有一个想头。接下来说一下我这么长时间内我理解的终极方案,截至本文发出来为止把,可能未来有更好的方案,甚至官网有什么更好的方案。那么就是网站端就是苹果cms。APP的解决方案就是GETAPP。模板的话 哪个加载快 用哪个。资源的话 采集就是官采+解析播放,现在市面上的解析其实对于一般用户来说是足够的。如果磁盘够用的话,可以尝试采集一点资源站,挑一些广告不是很多,资源比较齐全的。曾经的话 我推荐黑木耳资源,但是现在加入了广告,资源质量不是很好了,这个就智者见智了。
搭建苹果cms的一些感受 以下文字仅仅提供解决方案,所有图文字均源自网络,支持正版,人人有责。这也算是搭建苹果CMS很多次了,也有一些经验什么的了。这些简单说一些搭建苹果cms的终极方案,以及什么样的人适合搭建影视,什么样的人不适合影视首先就是如果你仅仅是为了自己看电影或者旁边人去看看电影,那么搭建苹果cms不是最佳的选择。现在市场上有很多开源的盒子,很多源。直接导入就可以用,如果不放心,可以投资的话 那么建议上NAS,或者其他的平替方案,总之苹果CMS,浪费时间。而且你搭建出来的不一定比别人好,别人切片,付费解析,各种方案一上,加载快。你反而得不偿失。接下来就是还有一种人不适合搞影视,就是如果搭建出是为了盈利,那么建议换一条赛道。这个盈利基本靠广告,但是能接到的广告,懂得都懂。如果你计划盈利的话 那么其实不太适合,建议换一条赛道。接下来什么样的人适合这个。首先就是如果你计划去公开网站进行SEO优化后引流之类的,那么影视适合,通过批量采集,吸引流量。其次就是如果是纯兴趣爱好,那么也适合,这里面门道有很多,很适合打法时间,或者说有一个想头。接下来说一下我这么长时间内我理解的终极方案,截至本文发出来为止把,可能未来有更好的方案,甚至官网有什么更好的方案。那么就是网站端就是苹果cms。APP的解决方案就是GETAPP。模板的话 哪个加载快 用哪个。资源的话 采集就是官采+解析播放,现在市面上的解析其实对于一般用户来说是足够的。如果磁盘够用的话,可以尝试采集一点资源站,挑一些广告不是很多,资源比较齐全的。曾经的话 我推荐黑木耳资源,但是现在加入了广告,资源质量不是很好了,这个就智者见智了。